Find the Solutions X Y to the System Equation

Solving Systems of Linear Equations

A system of linear equations is just a set of two or more linear equations.

In two variables $(x and y)$ , the graph of a system of two equations is a pair of lines in the plane.

There are three possibilities:

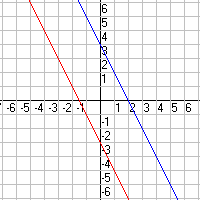
The lines intersect at zero points. (The lines are parallel.)
The lines intersect at exactly one point. (Most cases.)
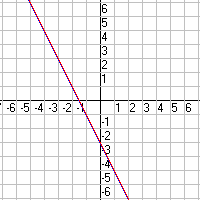
The lines intersect at infinitely many points. (The two equations represent the same line.)

Zero solutions:

$\begin{array}{l} y = - 2 x + 4 \\ y = - 2 x - 3 \end{array}$

One solution:

$\begin{array}{l} y = 0.5 x + 2 \\ y = - 2 x - 3 \end{array}$

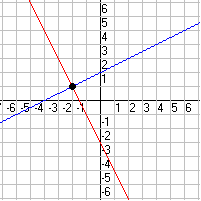
Infinitely many solutions:

$\begin{array}{l} y = - 2 x - 4 \\ y + 4 = - 2 x \end{array}$

There are a few different methods of solving systems of linear equations:

The Graphing Method . This is useful when you just need a rough answer, or you're pretty sure the intersection happens at integer coordinates. Just graph the two lines, and see where they intersect!

See the second graph above. The solution is where the two lines intersect, the point $(- 2, 1)$ .

The Substitution Method . First, solve one linear equation for $y$ in terms of $x$ . Then substitute that expression for $y$ in the other linear equation. You'll get an equation in $x$ . Solve this, and you have the $x$ -coordinate of the intersection. Then plug in $x$ to either equation to find the corresponding $y$ -coordinate. (If it's easier, you can start by solving an equation for $x$ in terms of $y$ , also – same difference!)

Example 1:

Solve the system ${\begin{cases} 3 x + 2 y = 16 \\ 7 x + y = 19 \end{cases}$

Solve the second equation for $y$ .

$y = 19 - 7 x$

Substitute $19 - 7 x$ for $y$ in the first equation and solve for $x$ .

$\begin{array}{l} 3 x + 2 (19 - 7 x) = 16 \\ 3 x + 38 - 14 x = 16 \\ - 11 x = - 22 \\ x = 2 \end{array}$

Substitute $2$ for $x$ in $y = 19 - 7 x$ and solve for $y$ .

$\begin{array}{l} y = 19 - 7 (2) \\ y = 5 \end{array}$

(2, 5)

The Linear Combination Method , aka The Addition Method , aka The Elimination Method. Add (or subtract) a multiple of one equation to (or from) the other equation, in such a way that either the $x$ -terms or the $y$ -terms cancel out. Then solve for $x$ (or $y$ , whichever's left) and substitute back to get the other coordinate.

Example 2:

Solve the system ${\begin{cases} 4 x + 3 y = - 2 \\ 8 x - 2 y = 12 \end{cases}$

Multiply the first equation by $- 2$ and add the result to the second equation.

$\begin{array}{l} - 8 x - 6 y = 4 \\ \underline{8 x - 2 y = 12} \\ - 8 y = 16 \end{array}$

Solve for $y$ .

$y = - 2$

Substitute for $y$ in either of the original equations and solve for $x$ .

$\begin{array}{l} 4 x + 3 (- 2) = - 2 \\ 4 x - 6 = - 2 \\ 4 x = 4 \\ x = 1 \end{array}$

The solution is $(1, - 2)$ .

The Matrix Method . This is really just the Linear Combination method, made simpler by shorthand notation.

Find the Solutions X Y to the System Equation

Source: https://www.varsitytutors.com/hotmath/hotmath_help/topics/solving-systems-of-linear-equations